2.3 神经网络的“齿轮”:张量运算
所有计算机程序最终都可以简化为二进制输入上的一些二进制运算(AND、OR、NOR等),与此类似,深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算(tensor operation),例如加上张量、乘以张量等。
在最开始的例子中,我们通过叠加Dense层来构建网络。Keras层的实例如下所示。
keras.layers.Dense(512, activation='relu')
这个层可以理解为一个函数,输入一个 2D张量,返回另一个 2D张量,即输入张量的新表示。具体而言,这个函数如下所示(其中W是一个 2D张量,b是一个向量,二者都是该层的属性)。
output = relu(dot(W, input) + b)
我们将上式拆开来看。这里有三个张量运算:输入张量和张量 W之间的点积运算(dot)、得到的 2D张量与向量b之间的加法运算(+)、最后的relu运算。relu(x)是max(x, 0)。
注意
虽然本节的内容都是关于线性代数表达式,但你却找不到任何数学符号。我发现,对于没有数学背景的程序员来说,如果用简短的 Python代码而不是数学方程来表达数学概念,他们将更容易掌握。所以我们自始至终将会使用 Numpy代码。
2.3.1 逐元素运算
relu运算和加法都是逐元素(element-wise)的运算,即该运算独立地应用于张量中的每个元素,也就是说,这些运算非常适合大规模并行实现(向量化实现,这一术语来自于 1970—1990年间向量处理器超级计算机架构)。如果你想对逐元素运算编写简单的 Python实现,那么可以用for循环。下列代码是对逐元素relu运算的简单实现。

根据同样的方法,你可以实现逐元素的乘法、减法等。
在实践中处理 Numpy数组时,这些运算都是优化好的 Numpy内置函数,这些函数将大量运算交给安装好的基础线性代数子程序( BLAS,basic linear algebra subprograms)实现(没装的话,应该装一个)。BLAS是低层次的、高度并行的、高效的张量操作程序,通常用 Fortran或 C语言来实现。
因此,在 Numpy中可以直接进行下列逐元素运算,速度非常快。

2.3.2 广播
上一节 naive_add的简单实现仅支持两个形状相同的 2D张量相加。但在前面介绍的Dense层中,我们将一个 2D张量与一个向量相加。如果将两个形状不同的张量相加,会发生什么?
如果没有歧义的话,较小的张量会被广播(broadcast),以匹配较大张量的形状。广播包含以下两步。
(1)向较小的张量添加轴(叫作广播轴),使其ndim与较大的张量相同。
(2)将较小的张量沿着新轴重复,使其形状与较大的张量相同。
来看一个具体的例子。假设 X的形状是 (32, 10),y的形状是 (10,)。首先,我们给 y添加空的第一个轴,这样 y的形状变为 (1, 10)。然后,我们将 y沿着新轴重复 32次,这样得到的张量Y的形状为(32, 10),并且Y[i, :] == y for i in range(0, 32)。现在,我们可以将X和Y相加,因为它们的形状相同。
在实际的实现过程中并不会创建新的 2D张量,因为那样做非常低效。重复的操作完全是虚拟的,它只出现在算法中,而没有发生在内存中。但想象将向量沿着新轴重复 10次,是一种很有用的思维模型。下面是一种简单的实现。

如果一个张量的形状是(a, b, … n, n+1, … m),另一个张量的形状是(n, n+1,… m),那么你通常可以利用广播对它们做两个张量之间的逐元素运算。广播操作会自动应用于从a到n-1的轴。
下面这个例子利用广播将逐元素的maximum运算应用于两个形状不同的张量。

2.3.3 张量点积
点积运算,也叫张量积(tensor product,不要与逐元素的乘积弄混),是最常见也最有用的张量运算。与逐元素的运算不同,它将输入张量的元素合并在一起。
在 Numpy、Keras、Theano和 TensorFlow中,都是用 *实现逐元素乘积。 TensorFlow中的点积使用了不同的语法,但在 Numpy和 Keras中,都是用标准的dot运算符来实现点积。
import numpy as np z = np.dot(x, y)
数学符号中的点(.)表示点积运算。
z=x.y
从数学的角度来看,点积运算做了什么?我们首先看一下两个向量 x和y的点积。其计算过程如下。

注意,两个向量之间的点积是一个标量,而且只有元素个数相同的向量之间才能做点积。
你还可以对一个矩阵 x和一个向量y做点积,返回值是一个向量,其中每个元素是 y和x的每一行之间的点积。其实现过程如下。

你还可以复用前面写过的代码,从中可以看出矩阵 -向量点积与向量点积之间的关系。
def naive_matrix_vector_dot(x, y):
z = np.zeros(x.shape[0])
for i in range(x.shape[0]):
z[i] = naive_vector_dot(x[i, :], y)
return z
注意,如果两个张量中有一个的 ndim大于 1,那么dot运算就不再是对称的,也就是说,dot(x, y)不等于dot(y, x)。
当然,点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。对于两个矩阵 x和y,当且仅当 x.shape[1] == y.shape[0]时,你才可以对它们做点积(dot(x, y))。得到的结果是一个形状为(x.shape[0], y.shape[1])的矩阵,其元素为x的行与y的列之间的点积。其简单实现如下。

为了便于理解点积的形状匹配,可以将输入张量和输出张量像图 2-5中那样排列,利用可视化来帮助理解。
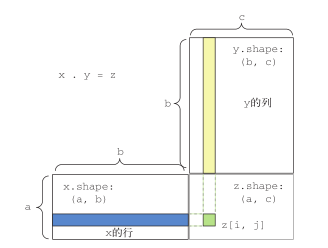
图 2-5 图解矩阵点积
图 2-5中,x、y和z都用矩形表示(元素按矩形排列)。x的行和y的列必须大小相同,因此x的宽度一定等于y的高度。如果你打算开发新的机器学习算法,可能经常要画这种图。
更一般地说,你可以对更高维的张量做点积,只要其形状匹配遵循与前面 2D张量相同的原则:
(a, b, c, d) . (d,) -> (a, b, c) (a, b, c, d) . (d, e) -> (a, b, c, e)
以此类推。
2.3.4 张量变形
第三个重要的张量运算是张量变形(tensor reshaping)。虽然前面神经网络第一个例子的Dense层中没有用到它,但在将图像数据输入神经网络之前,我们在预处理时用到了这个运算。
train_images = train_images.reshape((60000, 28 * 28))
张量变形是指改变张量的行和列,以得到想要的形状。变形后的张量的元素总个数与初始张量相同。简单的例子可以帮助我们理解张量变形。

经常遇到的一种特殊的张量变形是转置(transposition)。对矩阵做转置是指将行和列互换,使x[i, :]变为x[:, i]。

2.3.5 张量运算的几何解释
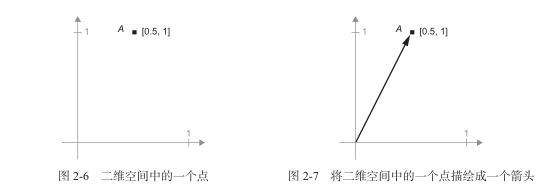
对于张量运算所操作的张量,其元素可以被解释为某种几何空间内点的坐标,因此所有的张量运算都有几何解释。举个例子,我们来看加法。首先有这样一个向量:
A = [0.5, 1]
它是二维空间中的一个点(见图 2-6)。常见的做法是将向量描绘成原点到这个点的箭头,如图 2-7所示。
假设又有一个点:B = [1, 0.25],将它与前面的A相加。从几何上来看,这相当于将两个向量箭头连在一起,得到的位置表示两个向量之和对应的向量(见图 2-8)。
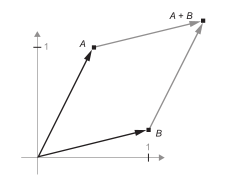
图 2-8 两个向量之和的几何解释
通常来说,仿射变换、旋转、缩放等基本的几何操作都可以表示为张量运算。举个例子,要将一个二维向量旋转 theta角,可以通过与一个 2×2矩阵做点积来实现,这个矩阵为R = [u, v],其中u和v都是平面向量:u = [cos(theta), sin(theta)],v = [-sin(theta), cos(theta)]。
2.3.6 深度学习的几何解释
前面讲过,神经网络完全由一系列张量运算组成,而这些张量运算都只是输入数据的几何变换。因此,你可以将神经网络解释为高维空间中非常复杂的几何变换,这种变换可以通过许多简单的步骤来实现。
对于三维的情况,下面这个思维图像是很有用的。想象有两张彩纸:一张红色,一张蓝色。将其中一张纸放在另一张上。现在将两张纸一起揉成小球。这个皱巴巴的纸球就是你的输入数据,每张纸对应于分类问题中的一个类别。神经网络(或者任何机器学习模型)要做的就是找到可以让纸球恢复平整的变换,从而能够再次让两个类别明确可分。通过深度学习,这一过程可以用三维空间中一系列简单的变换来实现,比如你用手指对纸球做的变换,每次做一个动作,如图 2-9所示。
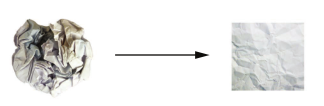
图 2-9 解开复杂的数据流形
让纸球恢复平整就是机器学习的内容:为复杂的、高度折叠的数据流形找到简洁的表示。现在你应该能够很好地理解,为什么深度学习特别擅长这一点:它将复杂的几何变换逐步分解为一长串基本的几何变换,这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通过变换使数据解开一点点——许多层堆叠在一起,可以实现非常复杂的解开过程。
