神经网络入门
本章包括以下内容:
- 神经网络的核心组件
- Keras简介
- 建立深度学习工作站
- 使用神经网络解决基本的分类问题与回归问题
本章的目的是让你开始用神经网络来解决实际问题。你将进一步巩固在第 2章第一个示例中学到的知识,还会将学到的知识应用于三个新问题,这三个问题涵盖神经网络最常见的三种使用场景:二分类问题、多分类问题和标量回归问题。
本章将进一步介绍神经网络的核心组件,即层、网络、目标函数和优化器;还会简要介绍Keras,它是贯穿本书的 Python深度学习库。你还将建立深度学习工作站,安装好 TensorFlow和Keras,并支持GPU。最后,我们将用三个介绍性示例深入讲解如何使用神经网络解决实际问题,
这三个示例分别是:
- 将电影评论划分为正面或负面(二分类问题)
- 将新闻按主题分类(多分类问题)
- 根据房地产数据估算房屋价格(回归问题)
学完本章,你将能够使用神经网络解决简单的机器问题,比如对向量数据的分类问题和回归问题。然后,你就可以从第 4章开始建立对机器学习更加具有原则性、理论性的理解。
3.1 神经网络剖析
前面几章介绍过,训练神经网络主要围绕以下四个方面。
- 层,多个层组合成网络(或模型)。
- 输入数据和相应的目标。
- 损失函数,即用于学习的反馈信号。
- 优化器,决定学习过程如何进行。
你可以将这四者的关系可视化,如图 3-1所示:多个层链接在一起组成了网络,将输入数据映射为预测值。然后损失函数将这些预测值与目标进行比较,得到损失值,用于衡量网络预测值与预期结果的匹配程度。优化器使用这个损失值来更新网络的权重。
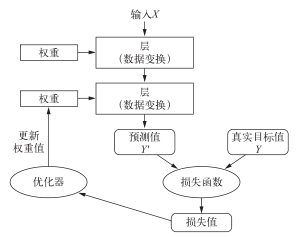
图 3-1 网络、层、损失函数和优化器之间的关系
我们来进一步研究层、网络、损失函数和优化器。
3.1.1 层:深度学习的基础组件
我们在第 2章中介绍过,神经网络的基本数据结构是层。层是一个数据处理模块,将一个或多个输入张量转换为一个或多个输出张量。有些层是无状态的,但大多数的层是有状态的,即层的权重。权重是利用随机梯度下降学到的一个或多个张量,其中包含网络的知识。
不同的张量格式与不同的数据处理类型需要用到不同的层。例如,简单的向量数据保存在形状为(samples, features)的 2D张量中,通常用密集连接层[densely connected layer,也叫全连接层(fully connected layer)或密集层(dense layer),对应于 Keras的Dense类]来处理。序列数据保存在形状为(samples, timesteps, features)的 3D张量中,通常用循环层(recurrent layer,比如 Keras的LSTM层)来处理。图像数据保存在 4D张量中,通常用二维卷积层(Keras的Conv2D)来处理。
你可以将层看作深度学习的乐高积木,Keras等框架则将这种比喻具体化。在 Keras中,构建深度学习模型就是将相互兼容的多个层拼接在一起,以建立有用的数据变换流程。这里层兼容性(layer compatibility)具体指的是每一层只接受特定形状的输入张量,并返回特定形状的输出张量。看看下面这个例子。
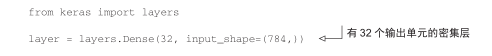
我们创建了一个层,只接受第一个维度大小为 784的 2D张量(第 0轴是批量维度,其大小没有指定,因此可以任意取值)作为输入。这个层将返回一个张量,第一个维度的大小变成了 32。
因此,这个层后面只能连接一个接受 32维向量作为输入的层。使用 Keras时,你无须担心兼容性,因为向模型中添加的层都会自动匹配输入层的形状,例如下面这段代码。
from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(32, input_shape=(784,))) model.add(layers.Dense(32))
其中第二层没有输入形状(input_shape)的参数,相反,它可以自动推导出输入形状等于上一层的输出形状。
3.1.2 模型:层构成的网络
深度学习模型是层构成的有向无环图。最常见的例子就是层的线性堆叠,将单一输入映射为单一输出。
但随着深入学习,你会接触到更多类型的网络拓扑结构。一些常见的网络拓扑结构如下。
- 双分支(two-branch)网络
- 多头(multihead)网络
- Inception模块
网络的拓扑结构定义了一个假设空间(hypothesis space)。你可能还记得第 1章里机器学习的定义:“在预先定义好的可能性空间中,利用反馈信号的指引来寻找输入数据的有用表示。”选定了网络拓扑结构,意味着将可能性空间(假设空间)限定为一系列特定的张量运算,将输入数据映射为输出数据。然后,你需要为这些张量运算的权重张量找到一组合适的值。
选择正确的网络架构更像是一门艺术而不是科学。虽然有一些最佳实践和原则,但只有动手实践才能让你成为合格的神经网络架构师。后面几章将教你构建神经网络的详细原则,也会帮你建立直觉,明白对于特定问题哪些架构有用、哪些架构无用。
3.1.3 损失函数与优化器:配置学习过程的关键
一旦确定了网络架构,你还需要选择以下两个参数。
- 损失函数(目标函数)——在训练过程中需要将其最小化。它能够衡量当前任务是否已成功完成。
- 优化器——决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降( SGD)的某个变体。
具有多个输出的神经网络可能具有多个损失函数(每个输出对应一个损失函数)。但是,梯度下降过程必须基于单个标量损失值。因此,对于具有多个损失函数的网络,需要将所有损失函数取平均,变为一个标量值。
选择正确的目标函数对解决问题是非常重要的。网络的目的是使损失尽可能最小化,因此,如果目标函数与成功完成当前任务不完全相关,那么网络最终得到的结果可能会不符合你的预期。想象一下,利用 SGD训练一个愚蠢而又无所不能的人工智能,给它一个蹩脚的目标函数:“将所有活着的人的平均幸福感最大化”。为了简化自己的工作,这个人工智能可能会选择杀死绝大多数人类,只留几个人并专注于这几个人的幸福——因为平均幸福感并不受人数的影响。这可能并不是你想要的结果!请记住,你构建的所有神经网络在降低损失函数时和上述的人工智能一样无情。因此,一定要明智地选择目标函数,否则你将会遇到意想不到的副作用。
幸运的是,对于分类、回归、序列预测等常见问题,你可以遵循一些简单的指导原则来选择正确的损失函数。例如,对于二分类问题,你可以使用二元交叉熵( binary crossentropy)损失函数;对于多分类问题,可以用分类交叉熵( categorical crossentropy)损失函数;对于回归问题,可以用均方误差( mean-squared error)损失函数;对于序列学习问题,可以用联结主义时序分类(CTC,connectionist temporal classification)损失函数,等等。只有在面对真正全新的研究问题时,你才需要自主开发目标函数。在后面几章里,我们将详细说明对于各种常见任务应选择哪种损失函数。

