4.3 数据预处理、特征工程和特征学习
除模型评估之外,在深入研究模型开发之前,我们还必须解决另一个重要问题:将数据输入神经网络之前,如何准备输入数据和目标?许多数据预处理方法和特征工程技术都是和特定领域相关的(比如只和文本数据或图像数据相关),我们将在后续章节的实例中介绍这些内容。现在我们要介绍所有数据领域通用的基本方法。
4.3.1 神经网络的数据预处理
数据预处理的目的是使原始数据更适于用神经网络处理,包括向量化、标准化、处理缺失值和特征提取。
1.向量化
神经网络的所有输入和目标都必须是浮点数张量(在特定情况下可以是整数张量)。无论处理什么数据(声音、图像还是文本),都必须首先将其转换为张量,这一步叫作数据向量化(data vectorization)。例如,在前面两个文本分类的例子中,开始时文本都表示为整数列表(代表单词序列),然后我们用 one-hot编码将其转换为float32格式的张量。在手写数字分类和预测房价的例子中,数据已经是向量形式,所以可以跳过这一步。
2.值标准化
在手写数字分类的例子中,开始时图像数据被编码为 0~255范围内的整数,表示灰度值。将这一数据输入网络之前,你需要将其转换为 float32格式并除以 255,这样就得到 0~1范围内的浮点数。同样,预测房价时,开始时特征有各种不同的取值范围,有些特征是较小的浮点数,有些特征是相对较大的整数。将这一数据输入网络之前,你需要对每个特征分别做标准化,使其均值为 0、标准差为 1。
一般来说,将取值相对较大的数据(比如多位整数,比网络权重的初始值大很多)或异质数据(heterogeneous data,比如数据的一个特征在 0~1范围内,另一个特征在 100~200范围内)输入到神经网络中是不安全的。这么做可能导致较大的梯度更新,进而导致网络无法收敛。为了让网络的学习变得更容易,输入数据应该具有以下特征。
- 取值较小:大部分值都应该在 0~1范围内。
- 同质性(homogenous):所有特征的取值都应该在大致相同的范围内。
此外,下面这种更严格的标准化方法也很常见,而且很有用,虽然不一定总是必需的(例如, 对于数字分类问题就不需要这么做)。
- 将每个特征分别标准化,使其平均值为 0。
- 将每个特征分别标准化,使其标准差为 1。
这对于 Numpy数组很容易实现。

3.处理缺失值
你的数据中有时可能会有缺失值。例如在房价的例子中,第一个特征(数据中索引编号为0的列)是人均犯罪率。如果不是所有样本都具有这个特征的话,怎么办?那样你的训练数据或测试数据将会有缺失值。
一般来说,对于神经网络,将缺失值设置为 0是安全的,只要 0不是一个有意义的值。网络能够从数据中学到 0意味着缺失数据,并且会忽略这个值。
注意,如果测试数据中可能有缺失值,而网络是在没有缺失值的数据上训练的,那么网络不可能学会忽略缺失值。在这种情况下,你应该人为生成一些有缺失项的训练样本:多次复制一些训练样本,然后删除测试数据中可能缺失的某些特征。
4.3.2 特征工程
特征工程(feature engineering)是指将数据输入模型之前,利用你自己关于数据和机器学习算法(这里指神经网络)的知识对数据进行硬编码的变换(不是模型学到的),以改善模型的效果。多数情况下,一个机器学习模型无法从完全任意的数据中进行学习。呈现给模型的数据应该便于模型进行学习。
我们来看一个直观的例子。假设你想开发一个模型,输入一个时钟图像,模型能够输出对应的时间(见图 4-3)。

图 4-3 从钟表上读取时间的特征工程
如果你选择用图像的原始像素作为输入数据,那么这个机器学习问题将非常困难。你需要用卷积神经网络来解决这个问题,而且还需要花费大量的计算资源来训练网络。
但如果你从更高的层次理解了这个问题(你知道人们怎么看时钟上的时间),那么可以为机器学习算法找到更好的输入特征,比如你可以编写 5行 Python脚本,找到时钟指针对应的黑色像素并输出每个指针尖的 (x, y)坐标,这很简单。然后,一个简单的机器学习算法就可以学会这些坐标与时间的对应关系。
你还可以进一步思考:进行坐标变换,将 (x, y)坐标转换为相对于图像中心的极坐标。这样输入就变成了每个时钟指针的角度 theta。现在的特征使问题变得非常简单,根本不需要机器学习,因为简单的舍入运算和字典查找就足以给出大致的时间。
这就是特征工程的本质:用更简单的方式表述问题,从而使问题变得更容易。它通常需要深入理解问题。
深度学习出现之前,特征工程曾经非常重要,因为经典的浅层算法没有足够大的假设空间来自己学习有用的表示。将数据呈现给算法的方式对解决问题至关重要。例如,卷积神经网络在 MNIST数字分类问题上取得成功之前,其解决方法通常是基于硬编码的特征,比如数字图像中的圆圈个数、图像中每个数字的高度、像素值的直方图等。
幸运的是,对于现代深度学习,大部分特征工程都是不需要的,因为神经网络能够从原始数据中自动提取有用的特征。这是否意味着,只要使用深度神经网络,就无须担心特征工程呢?并不是这样,原因有两点。
- 良好的特征仍然可以让你用更少的资源更优雅地解决问题。例如,使用卷积神经网络来读取钟面上的时间是非常可笑的。
- 良好的特征可以让你用更少的数据解决问题。深度学习模型自主学习特征的能力依赖于
- 大量的训练数据。如果只有很少的样本,那么特征的信息价值就变得非常重要。
4.4 过拟合与欠拟合
在上一章的三个例子(预测电影评论、主题分类和房价回归)中,模型在留出验证数据上的性能总是在几轮后达到最高点,然后开始下降。也就是说,模型很快就在训练数据上开始过拟合。过拟合存在于所有机器学习问题中。学会如何处理过拟合对掌握机器学习至关重要。
机器学习的根本问题是优化和泛化之间的对立。优化(optimization)是指调节模型以在训练数据上得到最佳性能(即机器学习中的学习),而泛化(generalization)是指训练好的模型在前所未见的数据上的性能好坏。机器学习的目的当然是得到良好的泛化,但你无法控制泛化,只能基于训练数据调节模型。
训练开始时,优化和泛化是相关的:训练数据上的损失越小,测试数据上的损失也越小。这时的模型是欠拟合(underfit)的,即仍有改进的空间,网络还没有对训练数据中所有相关模式建模。但在训练数据上迭代一定次数之后,泛化不再提高,验证指标先是不变,然后开始变差,即模型开始过拟合。这时模型开始学习仅和训练数据有关的模式,但这种模式对新数据来说是错误的或无关紧要的。
为了防止模型从训练数据中学到错误或无关紧要的模式,最优解决方法是获取更多的训练数据。模型的训练数据越多,泛化能力自然也越好。如果无法获取更多数据,次优解决方法是调节模型允许存储的信息量,或对模型允许存储的信息加以约束。如果一个网络只能记住几个模式,那么优化过程会迫使模型集中学习最重要的模式,这样更可能得到良好的泛化。
这种降低过拟合的方法叫作正则化(regularization)。我们先介绍几种最常见的正则化方法,然后将其应用于实践中,以改进 3.4节的电影分类模型。
4.4.1 减小网络大小
防止过拟合的最简单的方法就是减小模型大小,即减少模型中可学习参数的个数(这由层数和每层的单元个数决定)。在深度学习中,模型中可学习参数的个数通常被称为模型的容量(capacity)。直观上来看,参数更多的模型拥有更大的记忆容量(memorization capacity),因此能够在训练样本和目标之间轻松地学会完美的字典式映射,这种映射没有任何泛化能力。例如,拥有 500 000个二进制参数的模型,能够轻松学会 MNIST训练集中所有数字对应的类别——我们只需让 50 000个数字每个都对应 10个二进制参数。但这种模型对于新数字样本的分类毫无用处。始终牢记:深度学习模型通常都很擅长拟合训练数据,但真正的挑战在于泛化,而不是拟合。
与此相反,如果网络的记忆资源有限,则无法轻松学会这种映射。因此,为了让损失最小化,网络必须学会对目标具有很强预测能力的压缩表示,这也正是我们感兴趣的数据表示。同时请记住,你使用的模型应该具有足够多的参数,以防欠拟合,即模型应避免记忆资源不足。在容量过大与容量不足之间要找到一个折中。
不幸的是,没有一个魔法公式能够确定最佳层数或每层的最佳大小。你必须评估一系列不
同的网络架构(当然是在验证集上评估,而不是在测试集上),以便为数据找到最佳的模型大小。要找到合适的模型大小,一般的工作流程是开始时选择相对较少的层和参数,然后逐渐增加层的大小或增加新层,直到这种增加对验证损失的影响变得很小。
我们在电影评论分类的网络上试一下。原始网络如下所示。
代码清单 4-3 原始模型
from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(16, activation='relu', input_shape=(10000,))) model.add(layers.Dense(16, activation='relu')) model.add(layers.Dense(1, activation='sigmoid'))
现在我们尝试用下面这个更小的网络来替换它。
代码清单 4-4 容量更小的模型
model = models.Sequential() model.add(layers.Dense(4, activation='relu', input_shape=(10000,))) model.add(layers.Dense(4, activation='relu')) model.add(layers.Dense(1, activation='sigmoid'))
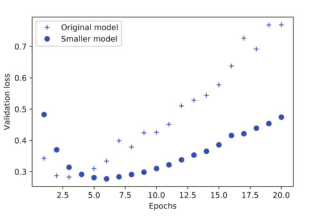
图 4-4比较了原始网络与更小网络的验证损失。圆点是更小网络的验证损失值,十字是原始网络的验证损失值(请记住,更小的验证损失对应更好的模型)。
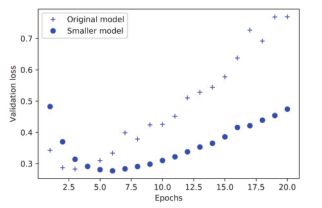
图 4-4 模型容量对验证损失的影响:换用更小的网络
如你所见,更小的网络开始过拟合的时间要晚于参考网络(前者 6轮后开始过拟合,而后者 4轮后开始),而且开始过拟合之后,它的性能变差的速度也更慢。
现在,为了好玩,我们再向这个基准中添加一个容量更大的网络(容量远大于问题所需)。
代码清单 4-5 容量更大的模型
model = models.Sequential() model.add(layers.Dense(512, activation='relu', input_shape=(10000,))) model.add(layers.Dense(512, activation='relu')) model.add(layers.Dense(1, activation='sigmoid'))
图 4-5显示了更大的网络与参考网络的性能对比。圆点是更大网络的验证损失值,十字是原始网络的验证损失值。
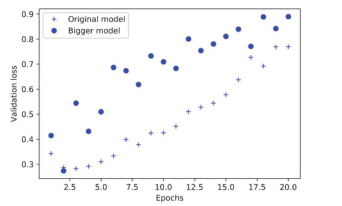
图 4-5 模型容量对验证损失的影响:换用更大的网络
更大的网络只过了一轮就开始过拟合,过拟合也更严重。其验证损失的波动也更大。
图 4-6同时给出了这两个网络的训练损失。如你所见,更大网络的训练损失很快就接近于零。网络的容量越大,它拟合训练数据(即得到很小的训练损失)的速度就越快,但也更容易过拟合(导致训练损失和验证损失有很大差异)。
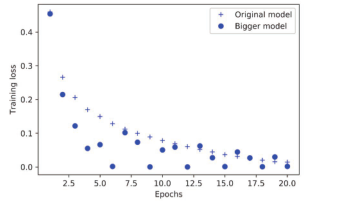
图 4-6 模型容量对训练损失的影响:换用更大的网络
4.4.2 添加权重正则化
你可能知道奥卡姆剃刀(Occam’s razor)原理:如果一件事情有两种解释,那么最可能正确的解释就是最简单的那个,即假设更少的那个。这个原理也适用于神经网络学到的模型:给定一些训练数据和一种网络架构,很多组权重值(即很多模型)都可以解释这些数据。简单模型比复杂模型更不容易过拟合。
这里的简单模型(simple model)是指参数值分布的熵更小的模型(或参数更少的模型,比如上一节的例子)。因此,一种常见的降低过拟合的方法就是强制让模型权重只能取较小的值,从而限制模型的复杂度,这使得权重值的分布更加规则(regular)。这种方法叫作权重正则化(weight regularization),其实现方法是向网络损失函数中添加与较大权重值相关的成本(cost)。这个成本有两种形式。
- L1正则化(L1 regularization):添加的成本与权重系数的绝对值[权重的 L1范数(norm)]成正比。
- L2正则化(L2 regularization):添加的成本与权重系数的平方(权重的 L2范数)成正比。神经网络的 L2正则化也叫权重衰减(weight decay)。不要被不同的名称搞混,权重衰减与 L2正则化在数学上是完全相同的。
在 Keras中,添加权重正则化的方法是向层传递权重正则化项实例(weight regularizer instance)作为关键字参数。下列代码将向电影评论分类网络中添加 L2权重正则化。
代码清单 4-6 向模型添加 L2权重正则化
from keras import regularizers
model = models.Sequential()
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
l2(0.001)的意思是该层权重矩阵的每个系数都会使网络总损失增加0.001 * weight_coefficient_value。注意,由于这个惩罚项只在训练时添加,所以这个网络的训练损失会比测试损失大很多。
图 4-7显示了 L2正则化惩罚的影响。如你所见,即使两个模型的参数个数相同,具有 L2正则化的模型(圆点)比参考模型(十字)更不容易过拟合。
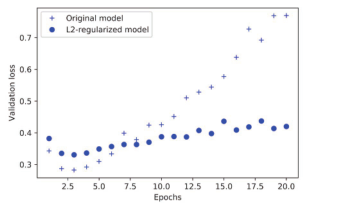
图 4-7 L2权重正则化对验证损失的影响
你还可以用 Keras中以下这些权重正则化项来代替 L2正则化。
代码清单 4-7 Keras中不同的权重正则化项

4.4.3 添加 dropout正则化
dropout是神经网络最有效也最常用的正则化方法之一,它是由多伦多大学的 Geoffrey Hinton和他的学生开发的。对某一层使用 dropout,就是在训练过程中随机将该层的一些输出特征舍弃(设置为 0)。假设在训练过程中,某一层对给定输入样本的返回值应该是向量[0.2, 0.5,1.3, 0.8, 1.1]。使用 dropout后,这个向量会有几个随机的元素变成 0,比如 [0, 0.5,1.3, 0, 1.1]。dropout比率(dropout rate)是被设为 0的特征所占的比例,通常在 0.2~0.5范围内。测试时没有单元被舍弃,而该层的输出值需要按 dropout比率缩小,因为这时比训练时有更多的单元被激活,需要加以平衡。
假设有一个包含某层输出的 Numpy矩阵layer_output,其形状为(batch_size,features)。训练时,我们随机将矩阵中一部分值设为 0。

测试时,我们将输出按 dropout比率缩小。这里我们乘以 0.5(因为前面舍弃了一半的单元)。
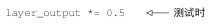
注意,为了实现这一过程,还可以让两个运算都在训练时进行,而测试时输出保持不变。这通常也是实践中的实现方式(见图 4-8)。
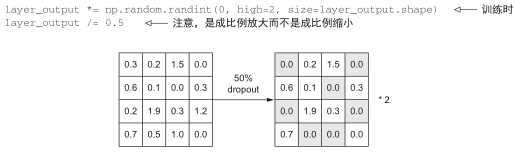
图 4-8 训练时对激活矩阵使用 dropout,并在训练时成比例增大。测试时激活矩阵保持不变
这一方法可能看起来有些奇怪和随意。它为什么能够降低过拟合? Hinton说他的灵感之一来自于银行的防欺诈机制。用他自己的话来说:“我去银行办理业务。柜员不停地换人,于是我问其中一人这是为什么。他说他不知道,但他们经常换来换去。我猜想,银行工作人员要想成功欺诈银行,他们之间要互相合作才行。这让我意识到,在每个样本中随机删除不同的部分神经元,可以阻止它们的阴谋,因此可以降低过拟合。”其核心思想是在层的输出值中引入噪声,打破不显著的偶然模式(Hinton称之为阴谋)。如果没有噪声的话,网络将会记住这些偶然模式。
在 Keras中,你可以通过 Dropout层向网络中引入 dropout,dropout将被应用于前面一层的输出。
model.add(layers.Dropout(0.5))
我们向 IMDB网络中添加两个Dropout层,来看一下它们降低过拟合的效果。
代码清单 4-8 向 IMDB网络中添加 dropout
model = models.Sequential() model.add(layers.Dense(16, activation='relu', input_shape=(10000,))) model.add(layers.Dropout(0.5)) model.add(layers.Dense(16, activation='relu')) model.add(layers.Dropout(0.5)) model.add(layers.Dense(1, activation='sigmoid'))
图 4-9给出了结果的图示。我们再次看到,这种方法的性能相比参考网络有明显提高。
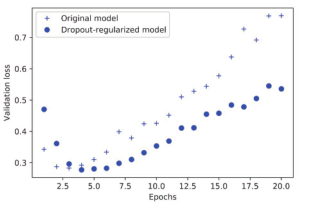
图 4-9 dropout对验证损失的影响
总结一下,防止神经网络过拟合的常用方法包括:
- 获取更多的训练数据
- 减小网络容量
- 添加权重正则化
- 添加 dropout
参见 Reddit网站上的讨论“AMA: We are the Google Brain team. We’d love to answer your questions about machine learning”。