6.2 理解循环神经网络
目前你见过的所有神经网络(比如密集连接网络和卷积神经网络)都有一个主要特点,那就是它们都没有记忆。它们单独处理每个输入,在输入与输入之间没有保存任何状态。对于这样的网络,要想处理数据点的序列或时间序列,你需要向网络同时展示整个序列,即将序列转换成单个数据点。例如,你在 IMDB示例中就是这么做的:将全部电影评论转换为一个大向量,然后一次性处理。这种网络叫作前馈网络(feedforward network)。
与此相反,当你在阅读这个句子时,你是一个词一个词地阅读(或者说,眼睛一次扫视一次扫视地阅读),同时会记住之前的内容。这让你能够动态理解这个句子所传达的含义。生物智能以渐进的方式处理信息,同时保存一个关于所处理内容的内部模型,这个模型是根据过去的信息构建的,并随着新信息的进入而不断更新。
循环神经网络(RNN,recurrent neural network)采用同样的原理,不过是一个极其简化的版本:它处理序列的方式是,遍历所有序列元素,并保存一个状态(state),其中包含与已查看内容相关的信息。实际上,RNN是一类具有内部环的神经网络(见图 6-9)。在处理两个不同的独立序列(比如两条不同的 IMDB评论)之间,RNN状态会被重置,因此,你仍可以将一个序列看作单个数据点,即网络的单个输入。真正改变的是,数据点不再是在单个步骤中进行处理,相反,网络内部会对序列元素进行遍历。
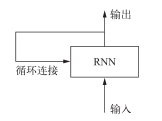
图 6-9 循环网络:带有环的网络
为了将环(loop)和状态的概念解释清楚,我们用 Numpy来实现一个简单 RNN的前向传递。这个 RNN的输入是一个张量序列,我们将其编码成大小为 (timesteps, input_features)的二维张量。它对时间步(timestep)进行遍历,在每个时间步,它考虑 t时刻的当前状态与 t时刻的输入[形状为 (input_ features,)],对二者计算得到t时刻的输出。然后,我们将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步,上一个时间步的输出没有定义,所以它没有当前状态。因此,你需要将状态初始化为一个全零向量,这叫作网络的初始状态(initial state)。
RNN的伪代码如下所示。
代码清单 6-19 RNN伪代码

你甚至可以给出具体的函数f:从输入和状态到输出的变换,其参数包括两个矩阵(W和U)和一个偏置向量。它类似于前馈网络中密集连接层所做的变换。
代码清单 6-20 更详细的 RNN伪代码
state_t = 0
for input_t in input_sequence:
output_t = activation(dot(W, input_t) + dot(U, state_t) + b)
state_t = output_t
为了将这些概念的含义解释得更加清楚,我们为简单 RNN的前向传播编写一个简单的 Numpy实现。
代码清单 6-21 简单 RNN的 Numpy实现

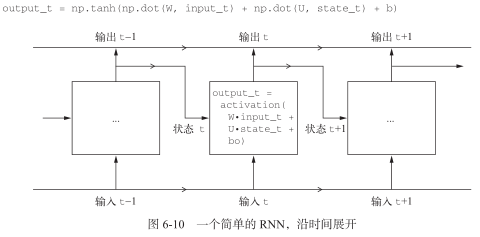
足够简单。总之,RNN是一个for循环,它重复使用循环前一次迭代的计算结果,仅此而已。当然,你可以构建许多不同的RNN,它们都满足上述定义。这个例子只是最简单的RNN表述之一。RNN的特征在于其时间步函数,比如前面例子中的这个函数(见图 6-10)。
注意
本例中,最终输出是一个形状为(timesteps, output_features)的二维张量,其中每个时间步是循环在 t时刻的输出。输出张量中的每个时间步 t包含输入序列中时间步0~t的信息,即关于全部过去的信息。因此,在多数情况下,你并不需要这个所有输出组成的序列,你只需要最后一个输出(循环结束时的 output_t),因为它已经包含了整个序列的信息。
6.2.1 Keras中的循环层
上面 Numpy的简单实现,对应一个实际的 Keras层,即SimpleRNN层。
from keras.layers import SimpleRNN
二者有一点小小的区别: SimpleRNN层能够像其他 Keras层一样处理序列批量,而不是像 Numpy示例那样只能处理单个序列。因此,它接收形状为 (batch_size, timesteps,input_features)的输入,而不是(timesteps, input_features)。
与 Keras中的所有循环层一样,SimpleRNN可以在两种不同的模式下运行:一种是返回每个时间步连续输出的完整序列,即形状为 (batch_size, timesteps, output_features)的三维张量;另一种是只返回每个输入序列的最终输出,即形状为 (batch_size, output_features)的二维张量。这两种模式由 return_sequences这个构造函数参数来控制。我们来看一个使用SimpleRNN的例子,它只返回最后一个时间步的输出。


下面这个例子返回完整的状态序列。

为了提高网络的表示能力,将多个循环层逐个堆叠有时也是很有用的。在这种情况下,你需要让所有中间层都返回完整的输出序列。


接下来,我们将这个模型应用于 IMDB电影评论分类问题。首先,对数据进行预处理。
代码清单 6-22 准备 IMDB数据

我们用一个Embedding层和一个SimpleRNN层来训练一个简单的循环网络。
代码清单 6-23 用Embedding层和SimpleRNN层来训练模型
from keras.layers import Dense
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
接下来显示训练和验证的损失和精度(见图 6-11和图 6-12)。
代码清单 6-24 绘制结果
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
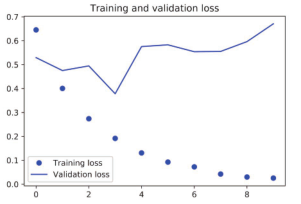
图 6-11 将SimpleRNN应用于 IMDB的训练损失和验证损失
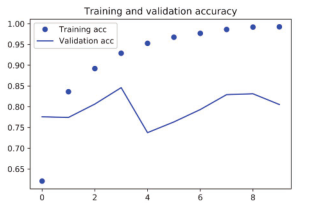
图 6-12 将SimpleRNN应用于 IMDB的训练精度和验证精度
提醒一下,在第 3章,处理这个数据集的第一个简单方法得到的测试精度是 88%。不幸的是,与这个基准相比,这个小型循环网络的表现并不好(验证精度只有 85%)。问题的部分原因在于,输入只考虑了前 500个单词,而不是整个序列,因此,RNN获得的信息比前面的基准模型更少。另一部分原因在于,SimpleRNN不擅长处理长序列,比如文本。
其他类型的循环层的表现要好得多。我们来看几个更高级的循环层。
6.2.2 理解 LSTM层和 GRU层
SimpleRNN并不是 Keras中唯一可用的循环层,还有另外两个: LSTM和GRU。在实践中总会用到其中之一,因为SimpleRNN通常过于简化,没有实用价值。SimpleRNN的最大问题是,在时刻t,理论上来说,它应该能够记住许多时间步之前见过的信息,但实际上它是不可能学到这种长期依赖的。其原因在于梯度消失问题(vanishing gradient problem),这一效应类似于在层数较多的非循环网络(即前馈网络)中观察到的效应:随着层数的增加,网络最终变得无法训练。Hochreiter、Schmidhuber和 Bengio在 20世纪 90年代初研究了这一效应的理论原因。LSTM层和GRU层都是为了解决这个问题而设计的。
先来看LSTM层。其背后的长短期记忆(LSTM,long short-term memory)算法由 Hochreiter和 Schmidhuber在 1997年开发,是二人研究梯度消失问题的重要成果。
LSTM层是SimpleRNN层的一种变体,它增加了一种携带信息跨越多个时间步的方法。假设有一条传送带,其运行方向平行于你所处理的序列。序列中的信息可以在任意位置跳上传送带,然后被传送到更晚的时间步,并在需要时原封不动地跳回来。这实际上就是 LSTM的原理:它保存信息以便后面使用,从而防止较早期的信号在处理过程中逐渐消失。
为了详细了解 LSTM,我们先从 SimpleRNN单元开始讲起(见图 6-13)。因为有许多个权重矩阵,所以对单元中的W和U两个矩阵添加下标字母o(Wo和Uo),表示输出。
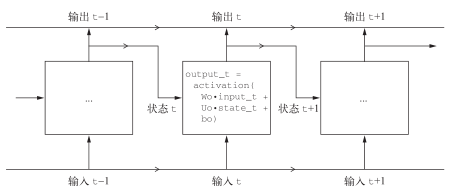
图 6-13 讨论LSTM层的出发点:SimpleRNN层
我们向这张图像中添加额外的数据流,其中携带着跨越时间步的信息。它在不同的时间步的值叫作Ct,其中C表示携带(carry)。这些信息将会对单元产生以下影响:它将与输入连接和循环连接进行运算(通过一个密集变换,即与权重矩阵作点积,然后加上一个偏置,再应用一个激活函数),从而影响传递到下一个时间步的状态(通过一个激活函数和一个乘法运算)。从概念上来看,携带数据流是一种调节下一个输出和下一个状态的方法(见图 6-14)。到目前为止都很简单。
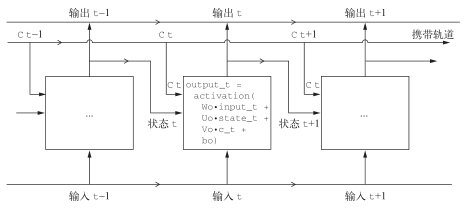
图 6-14 从SimpleRNN到LSTM:添加一个携带轨道
下面来看这一方法的精妙之处,即携带数据流下一个值的计算方法。它涉及三个不同的变换,这三个变换的形式都和SimpleRNN单元相同。
y = activation(dot(state_t, U) + dot(input_t, W) + b)
但这三个变换都具有各自的权重矩阵,我们分别用字母 i、j和k作为下标。目前的模型架构如下所示(这可能看起来有些随意,但请多一点耐心)。
代码清单 6-25 LSTM架构的详细伪代码(1/2)
output_t = activation(dot(state_t, Uo) + dot(input_t, Wo) + dot(C_t, Vo) + bo) i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi) f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf) k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk)
对i_t、f_t和k_t进行组合,可以得到新的携带状态(下一个c_t)。
代码清单 6-26 LSTM架构的详细伪代码(2/2)
c_t+1 = i_t * k_t + c_t * f_t
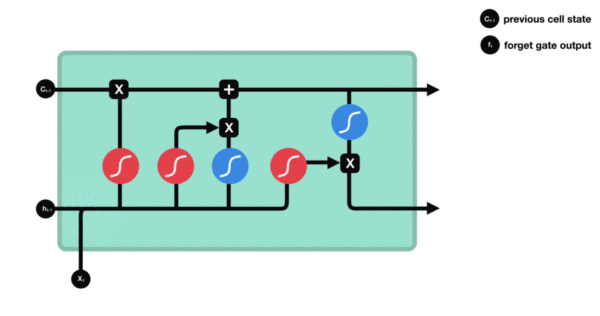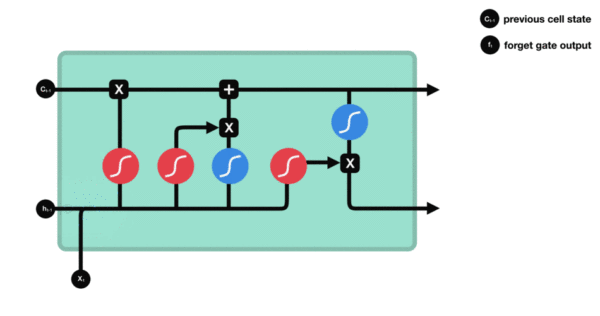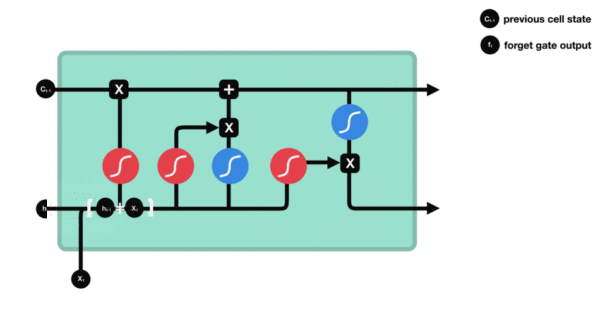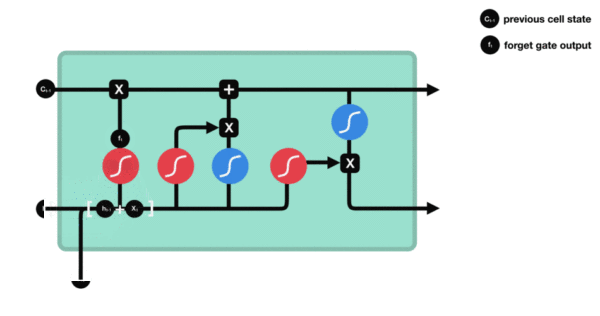
图 6-15给出了添加上述架构之后的图示。LSTM层的内容我就介绍完了。不算复杂吧?
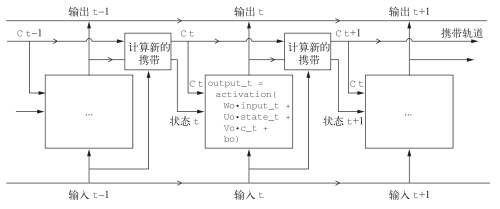
图 6-15 剖析 LSTM
如果要更哲学一点,你还可以解释每个运算的目的。比如你可以说,将 c_t和f_t相乘,是为了故意遗忘携带数据流中的不相关信息。同时,i_t和k_t都提供关于当前的信息,可以用新信息来更新携带轨道。但归根结底,这些解释并没有多大意义,因为这些运算的实际效果是由参数化权重决定的,而权重是以端到端的方式进行学习,每次训练都要从头开始,不可能为某个运算赋予特定的目的。RNN单元的类型(如前所述)决定了你的假设空间,即在训练期间搜索良好模型配置的空间,但它不能决定 RNN单元的作用,那是由单元权重来决定的。同一个单元具有不同的权重,可以实现完全不同的作用。因此,组成 RNN单元的运算组合,最好被解释为对搜索的一组约束,而不是一种工程意义上的设计。
对于研究人员来说,这种约束的选择(即如何实现 RNN单元)似乎最好是留给最优化算法来完成(比如遗传算法或强化学习过程),而不是让人类工程师来完成。在未来,那将是我们构建网络的方式。总之,你不需要理解关于 LSTM单元具体架构的任何内容。作为人类,理解它不应该是你要做的。你只需要记住 LSTM单元的作用:允许过去的信息稍后重新进入,从而解决梯度消失问题。
6.2.3 Keras中一个 LSTM的具体例子
现在我们来看一个更实际的问题:使用 LSTM层来创建一个模型,然后在 IMDB数据上训练模型(见图 6-16和图 6-17)。这个网络与前面介绍的SimpleRNN网络类似。你只需指定LSTM层的输出维度,其他所有参数(有很多)都使用 Keras默认值。Keras具有很好的默认值,无须手动调参,模型通常也能正常运行。
代码清单 6-27 使用 Keras中的LSTM层
from keras.layers import LSTM
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
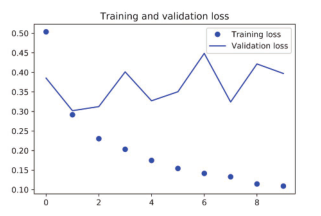
图 6-16 将LSTM应用于 IMDB的训练损失和验证损失
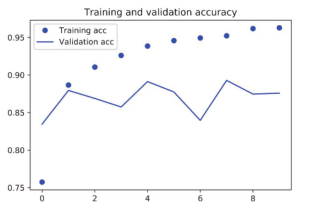
图 6-17 将LSTM应用于 IMDB的训练精度和验证精度
这一次,验证精度达到了 89%。还不错,肯定比 SimpleRNN网络好多了,这主要是因为LSTM受梯度消失问题的影响要小得多。这个结果也比第 3章的全连接网络略好,虽然使用的数据量比第 3章要少。此处在 500个时间步之后将序列截断,而在第 3章是读取整个序列。
但对于一种计算量如此之大的方法而言,这个结果也说不上是突破性的。为什么 LSTM不能表现得更好?一个原因是你没有花力气来调节超参数,比如嵌入维度或 LSTM输出维度。另一个原因可能是缺少正则化。但说实话,主要原因在于,适用于评论分析全局的长期性结构(这正是 LSTM所擅长的),对情感分析问题帮助不大。对于这样的基本问题,观察每条评论中出现了哪些词及其出现频率就可以很好地解决。这也正是第一个全连接方法的做法。但还有更加困难的自然语言处理问题,特别是问答和机器翻译,这时 LSTM的优势就明显了。
6.2.4 小结
现在你已经学会了以下内容。
- 循环神经网络(RNN)的概念及其工作原理。
- 长短期记忆(LSTM)是什么,为什么它在长序列上的效果要好于普通 RNN。
- 如何使用 Keras的 RNN层来处理序列数据。
接下来,我们将介绍 RNN几个更高级的功能,这可以帮你有效利用深度学习序列模型。